论文：Bell Nonlocality in Classical Systems Coexisting with Other System Types

Chiribella, G., Giannelli, L., Scandolo, C.M., 2024. Bell Nonlocality in Classical Systems Coexisting with Other System Types. Phys. Rev. Lett. 132, 190201. https://doi.org/10.1103/PhysRevLett.132.190201

The paper designed a toy model, which

(i) includes classical theory as a subtheory,
(ii) allows classical systems to be entangled with another type of system, called anticlassical.

In general classical theory, measurement outcomes cannot be regarded as predetermined by the state of an underlying reality.

The Classical Model

The realistic interpretation of classical theory:

• Physical systems have well-defined properties, even if these properties remain unknown to an observer.
• Measurements can reveal preexsisting properties.

Example:
A simple harmonic oscillator: a mass attached to a spring.
The position of the mass , its velocity , and the potential energy stored in the spring all have definite values at any given moment.
A precise equation describes the system:

$$m \frac{d^2 x}{dt^2} = -kx$$

Classical model: A special case of an operational probabilistic theory (OPT).

• The pure states of every given system are perfectly distinguishable through a single measurement;
• The pure states of every composite system are the products of pure states of the component systems;
• All permutations of the set of pure states are valid physical transformations.

Description:

• State: A classical theory with distinguishable pure states is called a dit. A mixed state in this theory is a probabilistic distribution.
• Transformations: Reversible trans are permutations; noisy trans are described by transition probabilities .
• Measurement: n matrix form, an output-determined measurement is a POVM. Born’s rule.

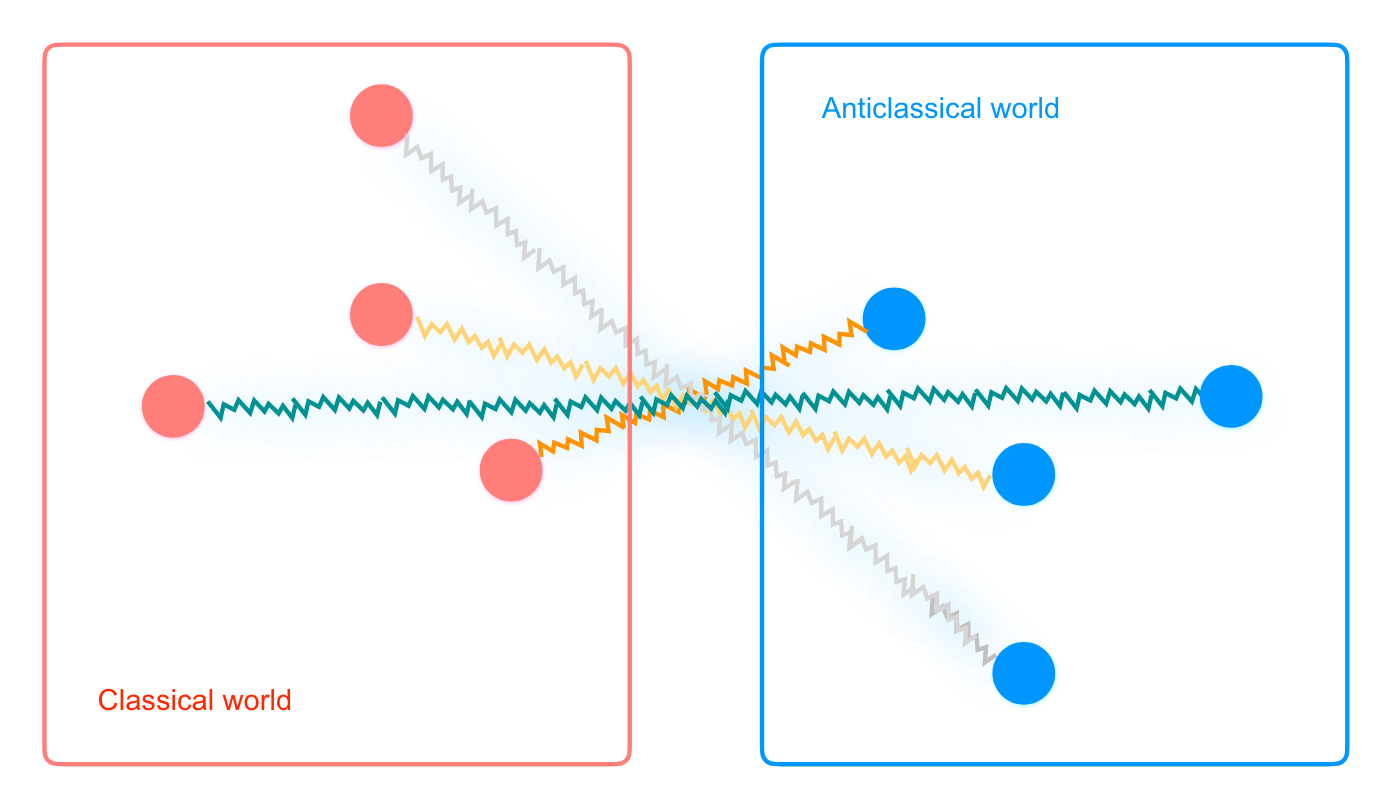
The Anticlassical model

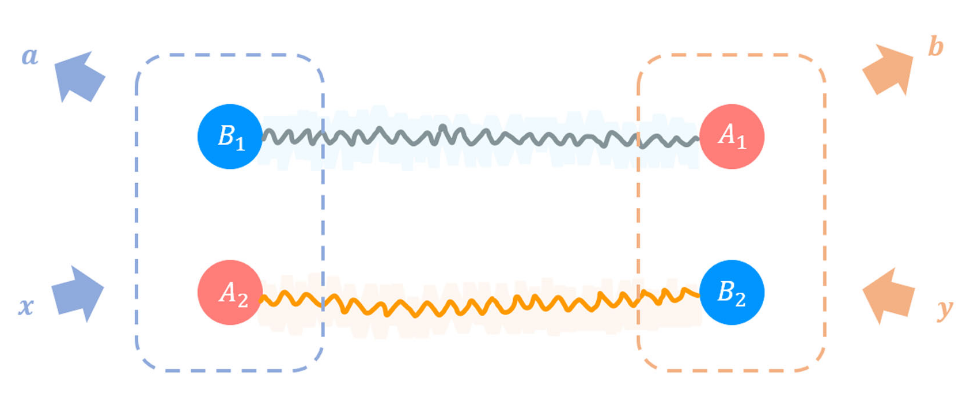
Consider a toy model: a classical system entangled with a “anti-classical” model.

The anti-classical-classical model is like an antiparticle-particle model.
Like paired particle and antiparticle, paired classical system and anti-classical system also have a well-defined parity.

Purification of the composite system:

From a pure entangled state of a bit-antibit pair:

$$|\Psi\rangle=\sqrt{p}|0\rangle|0\rangle+\sqrt{1-p}|1\rangle|1\rangle$$

Discarding the antibit, we have a mixed classical state:

$$\rho=p|0\rangle\langle 0|+(1-p)| 1\rangle\langle 1|$$

If the classical state is ontic, then it is always a pure state.
This corresponds to a separable state between classical bit and antibit.
So if the bit and antibit are entangled, there is no ontic classical model for the bit part.
The realistic interpretation can be falsified if classical systems exist alongside other types of physical systems.

Classical pure states are “ontic,” while classical mixed states are “epistemic”.
Ontic: These states describe the intrinsic nature of things, regardless of our knowledge or perception.
Epistemic: The probability distribution describing the uncertainty in a parameter’s value is an epistemic state.

The violation of Bell’s inequality

• Observer only has access to the classical part: No difference from a classical realistic interpretation.

• Observer has access to both parts: non-classical features, such as violations of Bell’s inequality.

With two pairs of bit-antibit, Alice and Bob can reproduce the results of arbitrary single-qubit measurements performed locally on a 2-qubit maximally entangled state.