Magic and Classical Simulation

Magic是量子计算中的一种资源。众所周知，没有Magic的量子线路可以被经典有效模拟。
而对于另一种资源，量子纠缠，张量网络算法可以有效模拟纠缠不太大的系统。更精确的说法是可以利用局域张量之间的bond维度截断来有效模拟area law的纠缠。
Magic作为度量量子计算资源的另一种度量，是否也可以设计一种算法，使得对于Magic随线路深度增长不太快的系统能够有效截断？
这篇讨论一下现有的一些经典模拟magic不太大的系统的算法。

Magic is a resource in quantum computing. It is well known that quantum circuits without Magic can be simulated efficiently by classical algorithms.
For the other resource, quantum entanglement, tensor network algorithms can effectively calculate systems with less entanglement. In a more precise way to say, a truncation of the bond dimension between local tensors can be utilized to effectively simulate entanglement that obeys AREA LAW.
Magic as an alternative metric for resources, is it also possible to design an algorithm that makes it possible to effectively truncate for systems where Magic does not grow too fast with depth？
This note discusses some of the existing algorithms for classically simulating not-so-magical systems.

Introduction

Stabilizer circuits are initialized in so-called stabilizer states and evolved by stabilizer operations, such that the system stays in a stabilizer state.
This kind of circuits can be efficiently classically simulated by virtue of the Gottesman-Knill theorem.
And stabilizer operations with many non-stabilizer operations can give the universality.
So the problem is weather system with stabilizer + few non-stabilizer operations can be classically simulated.

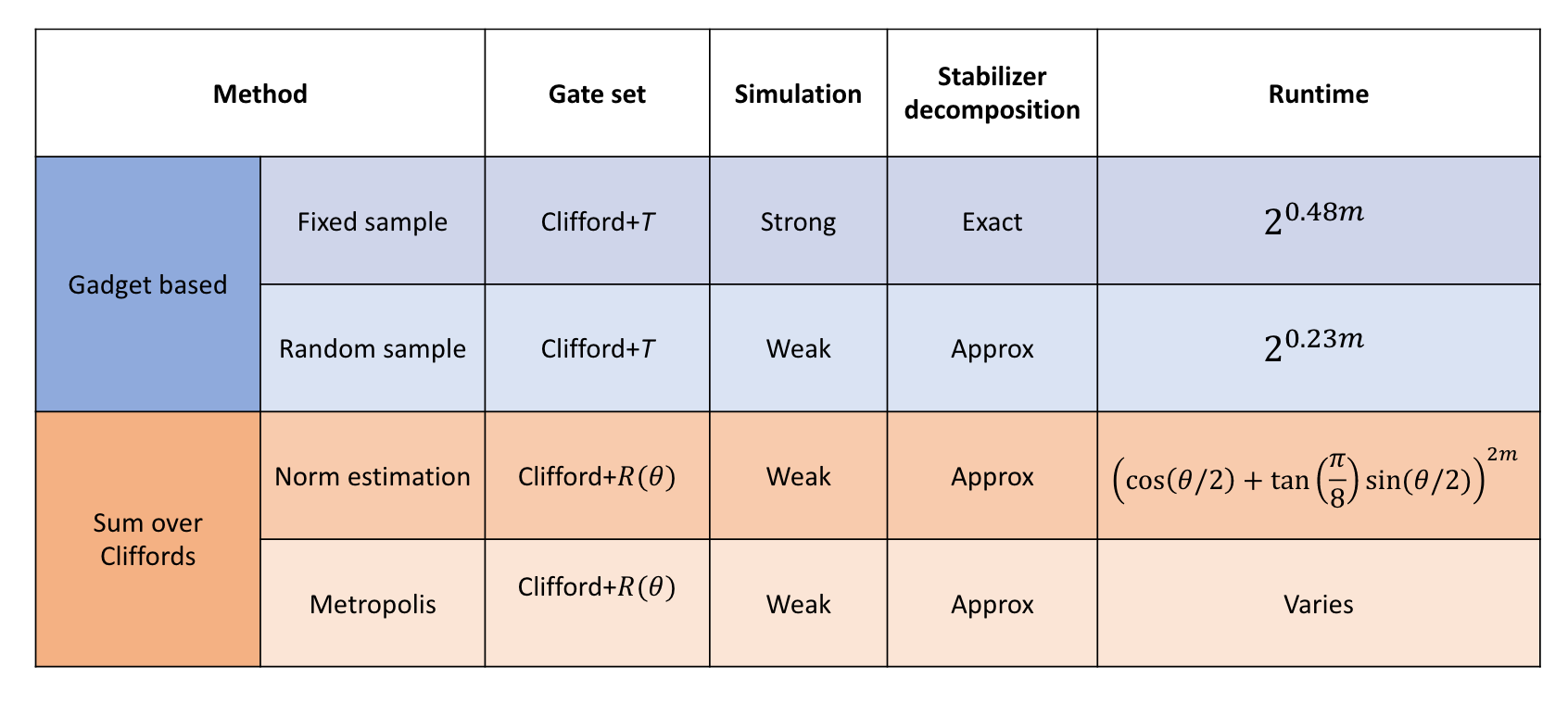
A direct algorithm¹ has runtime scaling polynomially with the number of qubits and exponentially with the number of input magic state qubits.

So we can perform an efficient classical simulation for circuits that has input magic state qubits sclaes logarithmically.

Faster classical simulation of nearly stabilizer circuits has two leading approaches: quasiprobability and stabilizer rank–based simulators. These simulators have runtime determined by different magic monotones.

Magic Monotones

Stabilizer theory:

• : pure n-qubit stabilizer state space.
• : mixed n-qubit stabilizer state space.
• $\mathcal{O}n\mathcal{E}\otimes \mathbb{I} \in \bar{S}{2n}\mathcal{E}\rho \in \bar{S}_n\mathcal{E}(\rho) \in \bar{S}_n$.
• : efficient classical simulation.

“Well-behaved” monotone :

• Faithfulness: iff .
• Monotonicity: for any free operation .
• Strong monoticity: (average monoticity)
  
  where are Kraus operatorsof a channel s.t. is stabilizer preserving. And .
• Convexity: .
• Submultiplicativity: .

• Stabilizer rank :
  The smallest integer such that can be written as a superposition of stabilizer states:

$$\chi(|\psi\rangle) = \min\{k, |\psi\rangle = \sum_{i=1}^k c_i |\phi_i\rangle\}$$

And we can define the approximate stabilizer rank : the smallest for s.t. .

• pure-state extent :

$$\xi(\Psi) := \min \{\|c\|_1^2, |\Psi\rangle=\sum_j c_j |\phi_j \rangle, |\phi_j \rangle \in S_n \}$$

is the n-bit pure stabilizer states.
is the l1-norm, which is the sum of all absolute values.

A dual optimization problem:

$$\xi(|\Psi\rangle) := \max \{|\langle \omega|\Psi \rangle|^2 , |\langle \omega|\phi\rangle|\leq 1, \forall|\phi\rangle \in S_n\}$$

Here, can be seen as a witness.

Stabilizer extent is the upper bound of the approximate stabilizer rank²:

$$\chi_\delta(|\psi\rangle) \leq 1+\xi(|\psi\rangle)/\delta^2$$

• Mixed-state extent :

$$\Xi(\rho) := \min \left\{\sum_jp_j\xi(\Psi_j), \rho = \sum_j p_j |\Psi_j\rangle \langle\Psi_j|\right\}$$

are pure states and are non-negative, .

• Robustness :

$$\mathcal{R}(\rho) := \min \left\{\|q\|_1, \rho=\sum_jq_j|\phi_j\rangle \langle \phi_j|, |\phi_j\rangle \in S_n\right\}$$

• Dyadic negativity :

$$\Lambda(\rho) := \min\{\|\alpha\|_1, \rho = \sum_j \alpha_j|L_j \rangle \langle R_j|, |L_j\rangle, |R_j\rangle \in S_n\}$$

A dyad means that each decomposed term relates two vectors in stabilizer space.

A dual optimization problem is a witnessing problem: define a set of witnesses:

$$\mathcal{W} := \{W, |\langle L|W|R\rangle|\leq 1, \forall |L\rangle,|R\rangle \in S_n\},$$

The dysdic negativity is then:

$$\Lambda (\rho) = \max \{\operatorname{Tr}[W\rho],W\in \mathcal{W}\}.$$

• Generalized robustness :

$$\Lambda^+ (\rho) := \max \{\operatorname{Tr}[W\rho], W\in \mathcal{W} \text{ and } W\geq 0\}.$$

Or to use the primal expression:

$$\Lambda^+(\rho) = \min\{\lambda, \rho\leq \lambda\sigma, \sigma\in \bar{S_n}\}.$$

Here is the mixed stabilizer state space.

The stabilizer rank-based simulation²

Summary:

• Idea: decomposition into a superposition of stabilizer states.
• Related monotones: stabilizer rank, stabilizer extent.
• On laptop: Stabilizer rank , qubits.
• Complexity: .
  
  Strong or weak: estimate a single output (with a small multiplicative error) or sample the output distribution (with a small statistical error). The runtime in the table ignores the polynomial terms.

A recent work by Chao Yin⁵ shows a special case of sampling high-temperature Gibbs states in polynimial time.
This implies that a high-T Gibbs state has magic grow logarithmically.

The quasi-probability-based simulation³⁴

Summary:

• Idea: using the frame representation of the quantum states.
• Related monotones: Mana (negativity in frame representation), robustness.
• Negativity leads to larger variance -> larger sample complexity.
• According to Hoeffding inequality, the number of samles that estimates output probability $pi\epsilon1-\deltas(\epsilon,\delta) \geq \frac{2}{\epsilon^2}\mathcal{M}{\rightarrow}^2\ln(2/\delta)$.
• The bound of total forward negativity scales exponentially in the number of magic qudits.
• So the sampling complexity is exponential of total magic depicted by .
  

¹:https://journals.aps.org/pra/abstract/10.1103/PhysRevA.70.052328, S. Aaronson and D. Gottesman, Phys. Rev. A 70, 052328, 2004
²:S. Bravyi et. al. “Simulation of Quantum Circuits by Low-Rank Stabilizer Decompositions.” Quantum 3,181 (2019). https://doi.org/10.22331/q-2019-09-02-181.
³: H. Pashayan, Joel J. Wallman, and Stephen D. Bartlett. “Estimating Outcome Probabilities of Quantum Circuits Using Quasiprobabilities.” Physical Review Letters 115, no. 7 (2015): 070501. https://doi.org/10.1103/PhysRevLett.115.070501.
⁴: Mark Howard, and Earl Campbell. “Application of a Resource Theory for Magic States to Fault-Tolerant Quantum Computing.” Physical Review Letters 118, no. 9 (March 3, 2017): 090501. https://doi.org/10.1103/PhysRevLett.118.090501.
⁵: Yin, Chao, and Andrew Lucas. “Polynomial-Time Classical Sampling of High-Temperature Quantum Gibbs States.” arXiv, May 29, 2023. http://arxiv.org/abs/2305.18514.