Contextuality 即是基本的量子非局域关联的体现，又可以对度量量子计算中的资源有所帮助。尤其是，state-dependednt的contextuality，和MBQC的资源密切相关。因此学习了一些。

Fundamental Question: Computational power可以由什么量来度量？

对于基于T + Cliffords 的计算体系，可以用 T gate的数量来描述。具有t个T门的线路可以被经典计算机以模拟。
因此这种模型可以用基于stabilizer theorem的Wigner negativity。
对于Measurement-based 计算体系，只需要考虑态和测量的性质。State dependent contextuality.
基于经典计算机没法在多项式时间计算而量子系统可以的一些问题也可以展示advantage。最简单的问题例如：query, quantum communication games.
而这两种简单的问题又和contextuality十分相关。

Contextuality

Reference of the section:
Abramsky, Samson, Rui Soares Barbosa, and Shane Mansfield. “Contextual Fraction as a Measure of Contextuality.” PRL 119, 5: 050504 (2017). https://doi.org/10.1103/PhysRevLett.119.050504.
Abramsky, Samson, and Adam Brandenburger. “The Sheaf-Theoretic Structure of Non-Locality and Contextuality.” New Journal of Physics 13, no. 11: 113036 (2011). https://doi.org/10.1088/1367-2630/13/11/113036.

Main Definition

A measurement senario is .

: A finite set of measurements.
: A finite set of measurement outcomes.
: A set of subsets in . Each is a set of measurements that can be performed together.
is called a measurement context.

An example: Bell senario.

Alice and Bob can each measure one of the qubits in a Bell pair.

They both perform one of the two possible measures: for Alice and for Bob. Each measurement gives either 0 or 1.

The measurement senario: $\begin{aligned} X &=\left\{a_1, a_2, b_1, b_2\right\}, \quad O=\{0,1\}^{\otimes 4} \\ \mathcal{M} &=\left\{\left\{a_1, b_1\right\},\left\{a_1, b_2\right\},\left\{a_2, b_1\right\},\left\{a_2, b_2\right\}\right\} \end{aligned}$

Empirical models: tables of data, specifying probability distributions over the joint outcomes of contexts.

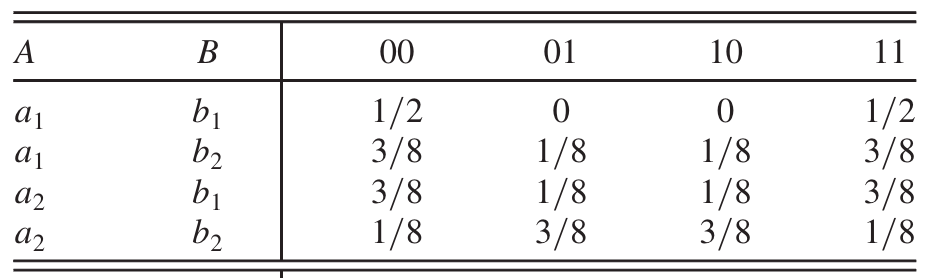
An example: an enpirical model for Bell senario, with at angle 0 and at .

For each row it is the distribution $eCC$.
The no-signaling (interactions can not be non-local) requires that is compatible on overlaps:
$\forall C, C^{\prime} \in \mathcal{M},\left.\quad e_C\right|{C \cap C^{\prime}}=\left.e{C^{\prime}}\right|{C \cap C^{\prime}}$
In this Bell senario, it means that Bob’s choice of measurement cannot influence Alice’s outcome.

Global section: A global distribution over all possible measurement out comes.

contextual: An empirical model is said to be contextual, if it is not compatible with a global section,
i.e. there is no global distribution on , such that .

ncHVM: Non-contextual hidden value model, assigns a definite outcome to each measurement, independent of the measurement context in which it appears.

The existence of a global section for an empirical model implies the existence of a ncHVM model which realizes it

Strong contextuality:
An empirical model is strongly contextual, if there is no global assignment such that .

存在这样的global assignment是比存在compatible的global section更弱的条件。因此“不存在”的条件就更强。
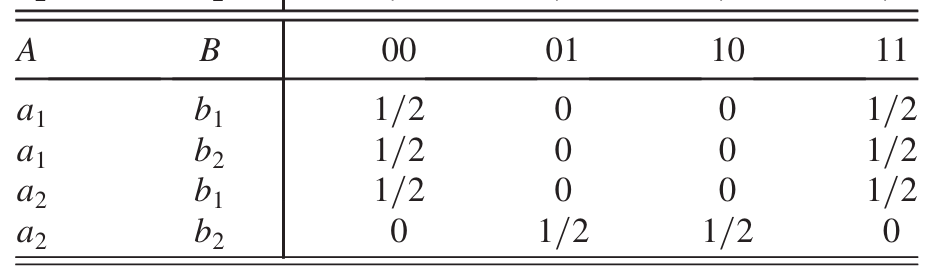
An example: PR box.

In Graph

设有个projector ，对应的graph就是把每个projector对应一个顶点（vertex），其中capatible的节点之间相互连接。

两个投影算符compatible，当且仅当它们互相正交（orthogonal）。
互相正交的测量同时进行，只能有一个结果是1.
因此对于所有projector构成的算符，期望值和图的结构有关。

Finding the global section - A linear problem

Incidence matrix: An matrix, with value .

: the number of global assignments, .
: the number of local assignments over contexts .

matrix element value:

$\mathbf{M}[\langle C, s\rangle, g]:= \begin{cases}1 & \text { if }\left.g\right|_C=s \\ 0 & \text { otherwise }\end{cases}$

For the example of Bell senario, the incidence matrix is .

In vector , an empirical model is , with conponents regarding probabilities. (相当于一个表格中的data被拉直了)

A global section is a vector . So the esistence of a global section is now the existence of a such that:

$\mathbf{M} \mathbf{d} = \mathbf{v}^e \quad \text{and} \quad \mathbf{d} \geq 0$

Measure of contextuality - Contextual fraction

Binary -> Quantitative measure of contextuality

For a given empirical model , it can be decomposed into a convex sum two empirical models: .

If is a non-contextual model, and is a strongly contextual model, then the value is called non-contextual fraction of , denoted by .

And the contextual fraction .

Calculation

To calculate , the incidence matrix is still useful. Assume a vector with weight , a linear program can calculate :

This is a linear programing (LP). This type of problems are NP, but not yet proven to be NP-complete.
LP can be related to graph - simplex algorithm.

Relation to Bell inequalities

A Bell inequality for a senario is given by :

$\mathbf{a} \cdot \mathbf{v}^e =\sum_{C \in \mathcal{M}, s \in O^C} \mathbf{a}[\langle C, s\rangle] e_C(s) \leq R$

: a non-negative bound for all non-contextual model. If the bound is saturated by some nc models, the inequality is said to be tight.
: a vector of real numbers.

Violation: The violation of Bell inequality by a model is .
And the normalized violation:

$\frac{\max \left\{0, \mathbf{a} \cdot \mathbf{v}^e-R\right\}}{\|\mathbf{a}\|-R}$

Theorem: The normalized violation by e of any Bell inequality is at most .

Problems for qubit

Contextuality 分为两种：

State-dependent contextuality: quantum state本身的性质，和 observables 无关。Measurable observables 的集合被指定为具有 consistent noncontextual value assignments.
The state is contextual, if no ncHVM reproduces all measurement statistics.
State-independent contextuality: for qubits, not a single consistent ncHVM for the Pauli observables exists. All states are contextual.

Qudits: systems of odd Hilbert space dimension.
对于qudits，free operations preserve the states to：

be stabilizer states
have a non-negative Wigner function
have a consistent ncHVM

However for qubits,

only the stabilizer is preserved.
Wigner non-negativity is not preserved under Cliffords.
ncHVM can not be defined.

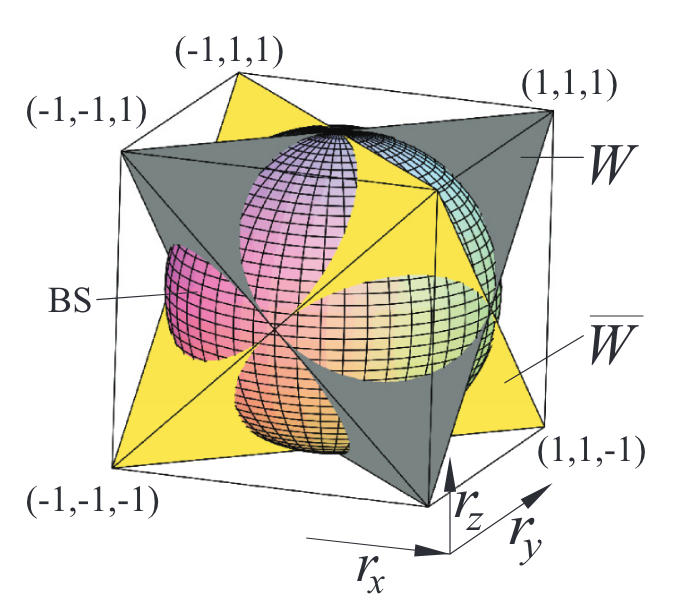
图为：1bit Bloch球和ncHVM以及非负Wigner function空间。

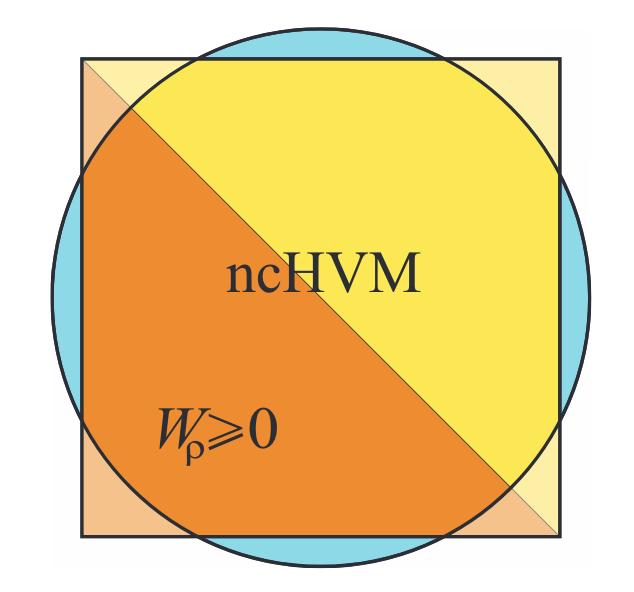
图为：n-bits 态空间大致的表示。

Qubit和qudit不同的原因：Heisenberg-Weyl operators behave differently！

Heisenberg-Weyl operators: all freely measureable observables.
For odd d, we have s.t. .
With the existence of , we can find a ncHVM for HW operators.
So for odd d, there is no state-independent contextuality.

Raussendorf, R., Browne, D.E., Delfosse, N., Okay, C., Bermejo-Vega, J., 2017. Contextuality and Wigner-function negativity in qubit quantum computation. Phys. Rev. A 95, 052334. https://doi.org/10.1103/PhysRevA.95.052334

As a non-linear resource in MBQC

Theorem: A MBQC with classical input and classical output that can deterministically evaluates a boolean function .If is nonlinear mod 2 in , then is strongly contextual.

Raussendorf, R., 2013. Contextuality in measurement-based quantum computation. Phys. Rev. A 88, 022322. https://doi.org/10.1103/PhysRevA.88.022322
Frembs, M., Roberts, S., Bartlett, S.D., 2018. Contextuality as a resource for measurement-based quantum computation beyond qubits. New J. Phys. 20, 103011. https://doi.org/10.1088/1367-2630/aae3ad

As a Resource for Qubit Computation with Magic States

PRL, 2017, Okay, Raussendorf.
Contextuality as a Resource for Models of Quantum Computation with Qubits

QSCI (quantum computation by state injection) scenario , with two constraints:

(C1) Reasource character. There exists a quantum state that does not exhibit contextuality with respect to measurements in .

(C2) Tomographic completeness. For any state , the expectation value of any Pauli observable can be inferred via the allowed operations.