QEC as a Thermo Engine

一篇把QEC过程当成热机的文章。可以用另一种途径解释许多问题。
Hint on之前提到的QEC ancilla 效率 - 和ancilla bath的温度有关。
Danageozian, Wilde, and Buscemi, “Thermodynamic Constraints on Quantum Information Gain and Error Correction.” https://link.aps.org/doi/10.1103/PRXQuantum.3.020318

0. 文章主要结论

文章得到的结论可以概括为三条：

• Measurement heat可以用 Groenewold information gain来bound。如果环境初始是热态，那么在测量过程中，系统流入环境的热量是被Groenewold information gain限制的。这里的gain可以是负值。
• QEC是被热力学第二定律限制的。这个是之前文章也有提到的结论，这里将之前结论进一步推广。
• 三个trade-off：三个量（max QEC fidelity，作为热机的thermodynamic efficiency，和测量的efficacy）之间互相制约。(i) 热机的效率超过Carnot循环越多，max QEC fidelity越小；(ii) 纠错时测量效率越大，热机效率越低。

1. Preliminaries

一些后面证明会用到的前置内容。

1.1 Quantum relative entropy

定义在希尔伯特空间上的两个半正定算符, 并且的support包含在的support里，，它们之间的quantum relative entropy:

$$D(M \| N):=\operatorname{Tr}[M \ln M]-\operatorname{Tr}[M \ln N]$$

这个量的作用是可以用来把熵增写成如下形式：

$$\begin{aligned} \Delta H(B)=&-\operatorname{Tr}_{B}\left[\sigma_{t}^{B} \ln \sigma_{t}^{B}\right]+\operatorname{Tr}_{B}\left[\sigma_{0}^{B} \ln \sigma_{0}^{B}\right] \\ =&-\operatorname{Tr}_{B}\left[\sigma_{t}^{B} \ln \sigma_{t}^{B}\right]+\operatorname{Tr}_{B}\left[\sigma_{t}^{B} \ln \sigma_{0}^{B}\right] -\operatorname{Tr}_{B}\left[\sigma_{t}^{B} \ln \sigma_{0}^{B}\right]+\operatorname{Tr}_{B}\left[\sigma_{0}^{B} \ln \sigma_{0}^{B}\right] \\ =& \operatorname{Tr}_{B}\left[\left(\sigma_{0}^{B}-\sigma_{t}^{B}\right) \ln \sigma_{0}^{B}\right]-D\left(\sigma_{t}^{B} \| \sigma_{0}^{B}\right) . \end{aligned}$$

1.2 Channel Efficacy

对于任何一个CP线性map ，可以引入一个efficacy ，表征在上的可逆性：

$$\mathscr{E}\left(\mathcal{N}^{A \rightarrow B} ; \rho^{A}\right):=\operatorname{Tr}\left[\left(\mathcal{N}^{A \rightarrow B}\right)^{\dagger} \circ \mathcal{N}^{A \rightarrow B}\left(\rho^{A}\right)\right]$$

Efficacy 可以和entropy联系起来，

$$\begin{aligned} H(B)_{\mathcal{N}(\rho)}-H(A)_{\rho} & \geq D\left(\rho^{A} \|\left(\mathcal{N}^{A \rightarrow B}\right)^{\dagger} \circ \mathcal{N}^{A \rightarrow B}\left(\rho^{A}\right)\right) \\ &=D\left(\rho^{A} \| \tilde{\rho}^{A}\right)-\ln \mathscr{E}\left(\mathcal{N}^{A \rightarrow B} ; \rho^{A}\right) \\ & \geq-\ln \mathscr{E}\left(\mathcal{N}^{A \rightarrow B} ; \rho^{A}\right) \end{aligned}$$

其中是normalized之后的dansity matrix，.

因为channel 不一定可逆，因此不一定是trace preserving的。所以进行normalize，使relative entropy两边都是density matrix。对于两边都是density matrix的情况，就可以表征距离，进而就是非负的。

1.3 关于量子测量

这篇文章中所说的测量，是指有一个quantum instrument ${\mathcal{N}x^A}{x\in \mathcal{X}}\rho^A\mathcal{N}_x^AAM$之间的一个unitary：

$$\mathcal{N}_{x}^{A}\left(\rho^{A}\right)=\operatorname{Tr}_{M}\left[U^{A M}\left(\rho^{A} \otimes \sigma^{M}\right)\left(U^{A M}\right)^{\dagger} P_{x}^{M}\right]$$

其中，是测量仪器的量子态。是希尔伯特空间中所有的线性、半正定、迹为1的算符。${P^MX}{x\in \mathcal{X}}M(\sigma^M,U^{AM},{P^MX}{x\in \mathcal{X}})$这样一个组合称之为一个间接测量模型（indirect measurement model）。

测量结果为的概率为：

$$p_X(x) := \operatorname{Tr}[\mathcal{N}_x^A(\rho^A)]$$

为了得到测量结果，再和一个经典寄存器耦合在一起：

$$\theta^{A X} \equiv \mathcal{N}^{A \rightarrow A X}(\rho^{A})=\sum_{x \in \mathcal{X}} \mathcal{N}_{x}^{A}(\rho^{A}) \otimes|x\rangle\langle x|^{X}.$$

加上经典寄存器，测量可以写作一个对整体的unitary：

$$\theta^{AMX}=U^{AMX}(\rho^A\otimes \sigma^M \otimes |0\rangle \langle 0|^X)(U^{AMX})^\dagger$$

其中的unitary是，。其中是经典寄存器上的投影算符。这里的trace掉就是前面式子中的.

1.4 Groenewold information

可以quantify一次测量获得的信息。定义是利用前述的instrument测量前后的熵减：

$$\begin{aligned} I_{G}\left(\left\{\mathcal{N}_{x}^{A}\right\}_{x} ; \rho^{A}\right) &:=H(A)_{\rho}-\sum_{x \in \mathcal{X}} p_{X}(x) H(A)_{\theta_{x}} \\ &=H(A)_{\rho}-H(A \mid X)_{\theta} \end{aligned}$$

对于投影测量，总是正的，但是在更一般的情况下有可能是负的。也可以定义另外的物理量quantum information gain来描述一次测量得到的信息，并且这个量不会是负值。

Information gain: 在Preskill的讲义中也定义了这样的量。待补充

1.5 Measurement Heat

Heat是热力学中一个重要的量。假设有系统和热库接触，构成一个封闭系统，那吸收的热量等于负的向耗散的热量：

$$-Q^{B\to S}_t = Q^{S\to B}_t = \Delta \langle \mathcal{H}^B\rangle := \langle \mathcal{H}^B\rangle_t - \langle \mathcal{H}^B\rangle_0$$

其中，, 是哈密顿量的期望值。

本文中的三个假设：

1. 系统和热库之间的演化是unitary的；
2. 初始时是温度为的热态；
3. 和初始时没有关联，是product state。

在这三个假设下，向耗散的热量有这样的关系（Reeb-Wolf formula）：

$$\beta Q_{t}^{S \rightarrow B}=-\Delta H(S)+I(S: B)+D\left(\rho_{t}^{B} \| \tau^{B}\right)$$

其中是互信息，是quantum relative energy。

考虑之前提到的测量，假设一个测量$(\tau^M,U^{AM},{P^MX}{x\in \mathcal{X}})MT_M$。这样，上面得到的热量关系就可以应用在测量中。（满足三个假设，unitary、热态和初始直积态）对这样一个测量有：

$$\begin{aligned} \beta Q_{\text {meas }} &:=\beta Q^{M \rightarrow A X} \\ &=\Delta H(A X)-I(A X: M)_{\theta}-D\left(\theta^{M} \| \tau^{M}\right) \\ &=H(A X)_{\theta}-H(A)_{\rho}-I(A X: M)_{\theta}-D\left(\theta^{M} \| \tau^{M}\right) \\ &=H(X)_{\theta}-I_{G}-I(A X: M)_{\theta}-D\left(\theta^{M} \| \tau^{M}\right) \end{aligned}$$

其中$IG({\mathcal{N}_x^A}{x\in \mathcal{X}}; \rho^A)=H(A)\rho - H(A|X)\thetaI_GAXM$吸收的热，反之亦然。

如果要计算进一步的bound可以假设，在测量之后，仍处于一个同样的热态，。这样就有。

这里的条件实际上是非常苛刻的，因为在一个一般的QEC中，进行syndrome测量之后，ancilla qubits的态一般都会有很大的变化。
这里的更进一步的bound可以这样理解：若ancilla不变，则后面就不需要通过接触低温热库来reset ancilla，也就没有那一步向低温热源的放热。因此，这里的measurement heat就可以取最大值。
这一项可以看成是测量前后的ancilla态之间的距离。

上面的式子又可以分解为两项：

$$\begin{aligned} \beta Q_{\text {meas }} &=\Delta H(A X)-I(A X: M)_{\theta} \\ &=: \beta Q_{\text {meas }}^{X}+\beta Q_{\text {meas }}^{A \mid X} \end{aligned}$$

其中的两项分别为：

$$\begin{aligned} &\beta Q_{\text {meas }}^{X}:=\Delta H(X)-I(X: M)_{\theta}=H(X \mid M)_{\theta}, \\ &\beta Q_{\text {meas }}^{A \mid X}:=\Delta H(A \mid X)-I(A: M \mid X)_{\theta} \end{aligned}$$

考虑到一开始被制备在，有$H(A|X)\rho = H(A)\rhoQ{\text {meas }}^{A \mid X}I_G=H(A)\rho - H(A|X)_\theta=-\Delta H(A|X)$ bound：

$$\beta Q_{\text {meas }}^{A \mid X}=-I_{G}-I(A: M \mid X)_{\theta} \leq-I_{G}$$

这就是的物理意义，代表系统在测量的时候从环境的吸热的一个上界。

2. QEC Stages

这里介绍的QEC各个步骤非常详细，可以借鉴来做一些AQEC的 simulation，分析各个步骤引入的误差。

设需要编码的态是，是它的一个纯化。另有ancilla系统和处于热态的系统,分别代表低温/高温的两个热库。除此之外还有经典寄存器负责储存测量结果或者控制量子操作。

整个QEC的过程可以分解成8个小步骤。见下图。

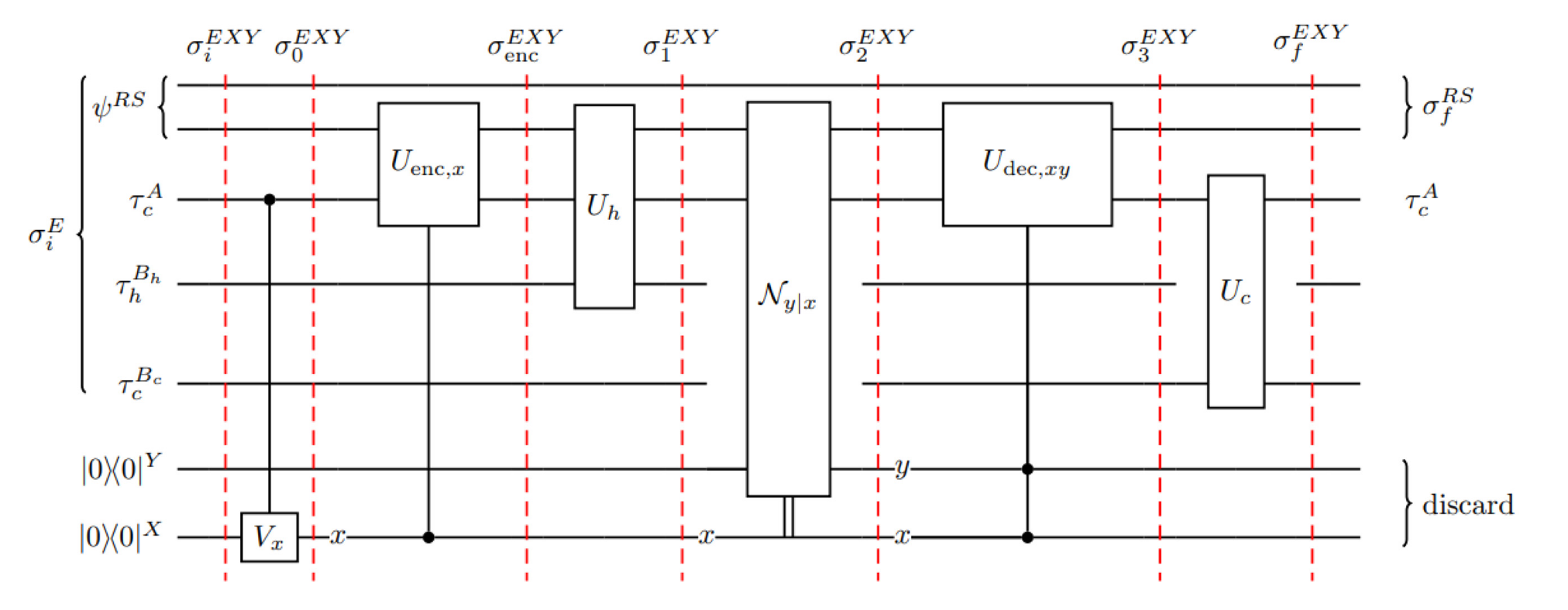
1. Initialization
   把所有的系统初始化在直积态：

$$\sigma_{i}^{E X Y}:=\psi^{R S} \otimes \tau_{c}^{A} \otimes \tau_{h}^{B_{h}} \otimes \tau_{c}^{B_{c}} \otimes|0\rangle\langle 0|^{X} \otimes \mid 0\rangle\langle 0|^{Y}.$$

其中 和 是系统, 和上的热态，温度分别是和。

1. Ancilla preparation
   为了encode ，需要把ancilla system 制备在能量本征态上，利用投影算符.其中的放到经典寄存器中存储。这一步结束之后的态变成了：

$$\sigma_{0}^{E X Y}:=\sum_{x} p_{X}(x) \frac{P_{x}^{A} \sigma_{i}^{E} P_{x}^{A}}{p_{X}(x)} \otimes|x\rangle\langle x|^{X} \otimes \mid 0\rangle\langle 0|^{Y}$$

实际上这一步相当于把总的Hilbert空间分成了label为x的子空间，为进行编码做准备。

1. Encoding

通过一个上的control unitary，把和耦合在一起形成编码态：

$$\sigma_{\mathrm{enc}, x}^{R S A}:=U_{\mathrm{enc}, x}^{S A}(|\psi\rangle\langle\psi|^{R S} \otimes \mid \varepsilon_{x}\rangle\langle\varepsilon_{x}|^{A})(U_{\mathrm{enc}, x}^{S A})^{\dagger}$$

1. Thermal-operation as noise

这里假设编码态空间收到热噪声的干扰，可以写成和处于温度为的热态的系统一起进行了一个unitary 操作：

$$\sigma_{1, x}^{R S A B_{h}}:=U^{S A B_{h}}\left(\sigma_{\mathrm{enc}, x}^{R S A} \otimes \tau_{h}^{B_{h}}\right)\left(U^{S A B_{h}}\right)^{\dagger}$$

如果是平时我们常见的完全随机rotation噪声，对应的就是无穷温度的情况。对于有限温度，还需要进一步分析。

1. Error-syndrome measurement

测量也相当于一个control unitary作用在上，测量结果储存在经典寄存器中。系统的态在测量之后变为：

$$\sigma_{2, x y}^{E}:=\frac{\mathcal{N}_{y \mid x}^{S A}\left(\sigma_{1, x}^{R S A B_{h}}\right)}{p_{Y \mid X}(y \mid x)} \otimes \tau_{c}^{B_{c}}$$

总的态变为：

$$\sigma_{2}^{E X Y}:=\sum_{x, y} p_{X Y}(x, y) \sigma_{2, x y}^{E} \otimes|x, y\rangle\langle x,y|^{X Y}$$

1. Error correction

Decoding就是根据经典信息选择对应的unitary操作来使的态尽可能接近初始的态。这一步也相当于一个对于系统的control unitary。

$$\sigma_{3}^{E X Y}=\sum p_{X Y}(x, y) \sigma_{3, x y}^{E} \otimes|x, y\rangle\langle x,y|^{X Y}$$

1. Resetting the ancilla system

为了构成一个循环，这时需要把ancilla system复位。这里就是之前一直没用的低温热库的作用：将和一起进行一个unitary，trace掉就能得到复位之后的态。如果是0K，那么ancilla就直接被带到基态。如果是有限温度，那么可能还处在一个混态。

$$\sigma_{f}^{E X Y}=U^{A B_{c}} \sigma_{3}^{E X Y}\left(U^{A B_{c}}\right)^{\dagger}$$

注意到这里其实可以使用SWAP门来实现复位：设cold bath的热态是$\tau^{Bc}_c=\otimes{i=1}^n \tau^{Bc^{(i)}}_cnAB_cU{\operatorname{SWAP}}|\psi \rangle \otimes |\phi\rangle = |\phi \rangle \otimes |\psi\rangle$）.

1. Discarding the classical registers

同样是为了构成一个循环，最后一步需要抹除两个经典寄存器的信息。这一步类似于对Maxwell’s Demon问题中经典信息的处理。

注意这个循环过程中，态的下标变化为
.

3. Entropic Analysis

接下来可以计算一下整个cycle下来，系统总的entropy的变化。

太长不看的结论：整个cycle下来，系统的entropy change是：
$H(E){\sigma_f}-H(E){\sigmai} = H(Y|X){\sigma2}-\sum_x p_X(x)I{G,x} - H(XY|E)_{\sigma_f}$

• 首先可以确定的是，$H(EXY){\sigma_0} = H(EXY){\sigmai}H(EXY){\sigma{\operatorname{enc}}}=H(EXY){\sigma_0}$。因为这两步都是unitary操作，不改变纠缠熵。
• 第一个非unitary的步骤就是syndrome测量。测量之后的entropy可以被拆分成和两部分：

$$\begin{aligned} H(EXY)_{\sigma_2} =& H(X) +H(EY|X)_{\sigma_2}\\ =& H(X) +\sum_x p_X(x)H(EY)_{\sigma_{2,x}} \end{aligned}$$

然后还可以继续拆分系统的entropy（回忆起条件熵可以写成的形式）：

$$\begin{aligned} H(E Y)_{\sigma_{2, x}} &=H(E)_{\sigma_{1, x}}-\left[H(E)_{\sigma_{1, x}}-H(E Y)_{\sigma_{2, x}}\right] \\ &=H(E)_{\sigma_{1, x}}-\left[H(E)_{\sigma_{1, x}}-H(Y)_{\sigma_{2, x}}-H(E \mid Y)_{\sigma_{2, x}}\right] \\ &=H(E)_{\sigma_{1, x}}+H(Y)_{\sigma_{2, x}}-I_{G}\left(\left\{\mathcal{N}_{y \mid x}^{S A}\right\}_{y} ; \sigma_{1, x}^{E}\right) \end{aligned}$$

最后一项后面会简写为.把上式带回上上式，得到：

$$\begin{aligned} &H(X)+\sum_{x} p_{X}(x)\left[H(E)_{\sigma_{1, x}}+H(Y)_{\sigma_{2, x}}-I_{G, x}\right] \\ &\quad=H(X)+H(E \mid X)_{\sigma_{1}}+H(Y \mid X)_{\sigma_{2}}-\sum_{x} p_{X}(x) I_{G, x} \\ &\quad=H(E X Y)_{\sigma_{1}}+H(Y \mid X)_{\sigma_{2}}-\sum_{x} p_{X}(x) I_{G, x} \end{aligned}$$

最后是利用了$H(EXY){\sigma_1} = H(EX){\sigma_1}$.

• 后面的几步操作仍然是unitary，不改变entropy。
• 最后一步discard 经典寄存器是会改变entropy的。这里的熵变是$H(E){\sigma_f}-H(EXY){\sigmaf}=-H(XY|E){\sigma_f}$.

---

也可以将熵变写成放热的形式。首先直接给出结论就是：

$$\begin{aligned} H(E)_{\sigma_{f}}-H(E)_{\sigma_{i}}=& S_{e}-\frac{Q_{h}}{k_{B} T_{h}}-\frac{Q_{c}}{k_{B} T_{c}} \\ &-I\left(R S: B_{h} B_{c}\right)_{\sigma_{f}}-\Gamma\left(B_{h} B_{c}\right)_{\sigma_{f}} \end{aligned}$$

其中，$SeRSRSRSRSS_e = H(RS){\sigma_f}$。

最后一项为：

$$\begin{aligned} \Gamma\left(B_{h} B_{c}\right)_{\sigma_{f}}:=& I\left(B_{h}: B_{c}\right)_{\sigma_{f}}+D\left(\sigma_{f}^{B_{h}} \| \tau_{h}^{B_{h}}\right) \\ &+D\left(\sigma_{f}^{B_{c}} \| \tau_{c}^{B_{c}}\right) \geq 0, \end{aligned}$$

推导过程：
主要思路是用互信息拆分总的系统的entropy。
首先，因为ancilla已经被复位，和系统其他部分没有关联了，所以可以拆出：

$$H(E)_{\sigma_{f}} \equiv H(R S A B_{h} B_{c})_{\sigma_{f}}=H\left(R S B_{h} B_{c}\right)_{\sigma_{f}}+H(A)_{\sigma_{f}}$$

然后，可以将两个热库和拆分出来：

$$\begin{aligned} H\left(R S B_{h} B_{c}\right)_{\sigma_{f}}=& H(R S)_{\sigma_{f}}+H\left(B_{h}\right)_{\sigma_{f}}+H\left(B_{c}\right)_{\sigma_{f}} \\ &-I\left(B_{h}: B_{c}\right)_{\sigma_{f}}-I\left(R S: B_{h} B_{c}\right)_{\sigma_{f}} . \end{aligned}$$

这样熵的变化就是：

$$\begin{aligned} H(E)_{\sigma_{f}}-H(E)_{\sigma_{i}}=& H(R S)_{\sigma_{f}}+\Delta H\left(B_{h}\right)_{\sigma_{f}} \\ &+\Delta H\left(B_{c}\right)_{\sigma_{f}}-I\left(R S: B_{h} B_{c}\right)_{\sigma_{f}} \\ &-I\left(B_{h}: B_{c}\right)_{\sigma_{f}} \end{aligned}$$

这里利用了初始时各个部分之间没有关联，是直积态，因此互信息为0.
最后利用前面Measurement Heat那一节用到的Reeb-Wolf formula，得到结果。

4. Efficiency-Fidelity Trade-off

4.1 Fano inequality

对于与其他部分之间的熵交换$Se = H(RS){\sigma_f}$，有quantum Fano inequality可以bound：

$$H(F_e)+(1-F_e)\ln (d^2-1) \geq S_e$$

其中，是二进制entropy。（只有两个状态的系统的enropy）就是初态和末态之间的Fidelity。
是总的态空间维度。

从这里可以看出，是精确QEC（）的必要条件，而不是充分条件。

4.2 Definition of thermodynamic efficiency of QEC engine

对于在两个热库之间运转的热机来说，如果没有feedback control，那么它的效率最大会接近Carnot热机效率 。而循环（回到初态）的条件其实就和QEC是一样的。

因此，可以分析QEC engine，把 的条件和 的条件联系在一起。

对QEC engine，效率的定义也是对外做的总功除以总的吸热：$\eta := -W{tot}/Q{input}$.接下来就计算一下一个QEC cycle中每一步的做功和吸热。

Note: QEC热机中的“working fluid”是系统。计算效率需要计算的是这个部分的做功和吸热。

内能：可以看做是哈密顿量的期望值， . 内能的变化就是吸放热$-Q{t}^{B \rightarrow S} \equiv Q{t}^{S \rightarrow B}=\Delta\left\langle\mathscr{H}^{B}\right\rangle:=\left\langle\mathscr{H}^{B}\right\rangle{t}-\left\langle\mathscr{H}^{B}\right\rangle{0}$

首先来分析一下系统的内能变化。注意到：

$$\Delta \mathscr{U}^{SA} = \Delta \mathscr{U}^{RSA} = \Delta \mathscr{U}^{RSAY}$$

第一个等号是因为用于纯化的reference system在整个过程中没变，。第二个等号是因为最后被抹除了。因此我们可以通过计算来得到，这样会比较容易。

仍然按照的顺序来计算每一步的做功和吸热。我们有：

$$\begin{aligned} \mathscr{U}_{0}^{R S A Y}-\mathscr{U}_{i}^{R S A Y}&=0, \\ \mathscr{U}_{\mathrm{enc}}^{R S A Y}-\mathscr{U}_{0}^{R S A Y}&=W_{\text {enc }}, \\ \mathscr{U}_{1}^{R S A Y}-\mathscr{U}_{\mathrm{enc}}^{R S A Y}&=Q_{h},\\ \mathscr{U}_{2}^{R S A Y}-\mathscr{U}_{1}^{R S A Y} &=\operatorname{Tr}\left[\left(\sigma_{2}^{R S A Y}-\sigma_{1}^{R S A Y}\right) \mathscr{H}^{R S A Y}\right]\\ &= W_{\text{meas}}+Q_{\text{meas}},\\ \mathscr{U}_{3}^{R S A Y}-\mathscr{U}_{2}^{R S A Y}&=W_{\text {dec }}, \\ \mathscr{U}_{f}^{R S A Y}-\mathscr{U}_{3}^{R S A Y}&=Q_{c}, \\ \mathscr{U}_{\text {erase }}^{R S A Y}-\mathscr{U}_{f}^{R S A Y}&=\left\langle\mathscr{H}^{Y}\right\rangle_{i}-\left\langle\mathscr{H}^{Y}\right\rangle_{f} \equiv Q_{\text {erase }}^{Y}. \end{aligned}$$

系统吸收的热量可以通过分析每一个的正负（正为吸热，负为放热），把所有为正值的加起来得到。

• 首先分析syndrome测量这一步的吸热。根据之前对measurement heat的分析，可以将其拆分：

$$Q_{\text{meas}} = Q_{\text {meas}}^{Y}+Q_{\text {meas }}^{R S A|Y}-k_{B} T_{m} D\left(\sigma_{2}^{M} \| \tau_{m}^{M}\right)$$

根据定义，有：

$$\begin{aligned} \frac{Q_{\text {meas }}^{Y}}{k_{B} T_{m}} &=\Delta H(Y \mid X)-I(Y: M \mid X)_{\sigma_{2}} \\ &=H(Y \mid X M)_{\sigma_{2}} \geq 0 \end{aligned}$$

• 对于，我们认为它是小于等于0，因为QEC要实现其功能就需要通过syndrome测量将entropy（information）传递到测量系统。

• 另外，由于我们研究的是高温/低温热库之间运行的热机，我们有。

• 对于抹除吸收的热量，我们认为，因为抹除需要和低温热库接触，回到ground state所以应该放热。

现在可以计算总吸热：

$$Q_{\text{input}} := Q_h+Q_{\text{meas}}^Y$$

如果QEC是接近完美的，那么内能的变化量就很小。而又可以证明infidelity $\epsilon \ll (Q{\text{input}}/2|\mathscr{H}^s|\infty)^2\left|\Delta \mathscr{U}^{R S A Y}\right| \ll Q_{\text{input}}$:

$$\begin{aligned} \left|\Delta \mathscr{U}^{R S}\right| &=\left|\operatorname{Tr}\left[\left(\sigma_{f}^{R S}-\sigma_{i}^{R S}\right) \mathscr{H}^{R S}\right]\right| \\ & \leq\left\|\sigma_{f}^{R S}-\sigma_{i}^{R S}\right\|_{1} \cdot\left\|\mathscr{H}^{R S}\right\|_{\infty} \\ & \leq 2\left\|\mathscr{H}^{S}\right\|_{\infty} \sqrt{\varepsilon} \end{aligned}$$

其中第一个不等式是Holder inequality，第二个不等式是由于对于entanglement fidelity between any and , .

p-norm: 对于实数，一个向量$\mathbf{x} =(x1, \dots ,x_n)|\mathbf{x}|_p:=\left(\sum{i=1}^n\left|xi\right|^p\right)^{1 / p}p \to \infty|\mathbf{x}|\infty = \max_i |x_i|$.

Holder’s inequality: 对于两个实数和，满足，和定义在度量空间上的两个函数，，有：
.

因此，对于近似完美的QEC情况，即可以忽略内能变化的情况，根据热力学第一定律我们有$W{\text{tot}} \approx -Q{tot}$，所以热机的效率也就是：

$$\eta:=-W_{\text {tot }} / Q_{\text {input }} \approx Q_{\text {tot }} / Q_{\text {input }}$$

Note: 这里直接把QEC当成完美的，完全忽略了AQEC的情况。如果考虑AQEC，则要考虑外界对系统做功如何计算。但这篇文章似乎没有计算过做功，还需要再调研一下。

推导triple-trade-off relation

假设与前提

本文的讨论是基于以下四个假设和一个前提的：

• 前提：系统中只用到一个cold bath ，它不仅被用来循环利用ancilla system，还用来reset 经典寄存器和。

• Assumption 1：足够大的fidelity。详见上一节结尾的讨论。

• Assumption 2：在抹除经典寄存器之前，中的熵比起中的熵可以忽略不计。$H(X|E){\sigma_f}\ll H(Y|EX){\sigma_f}$.
• Assumption 3：Landauer bound在实验的系统中可以近似达到。这个bound是关于抹除经典信息的，在关于麦克斯韦妖的讨论中出现。即$|Q{erase}^Y| \approx k_BT_cH(Y|X){\sigma_2}$.
• Assumption 4：在测量中，系统向经典比特的放热是Sufficient dissipation,即$|Q{meas}^{RSA|Y}|\geq \frac{T_c}{T_h}Q^Y{meas}$.