论文：测量引起的相变

在量子计算线路中，随机的两比特unitary可以积累纠缠，但是加入随机的local measurement会降低纠缠。
因此这两种操作交替出现在线路中可以出现一个相变。

Intro

总结一下测量相变（MIPT）的相关内容以及和AQEC的关系。
主要来源是这篇PRL文章。文章简洁清楚地介绍了MIPT并且给出了一个简单的数值结果。

基于线路的量子计算使用门操作来积累non-local纠缠。而对于量子系统的随机测量总是使纠缠丢失。
那么在一个反复作用门和随机测量的系统中，两种操作的竞争就会导致一个相变。这就是MIPT。
文中将2bits线路积累的纠缠称为“scrambling”，但是实则计算的量还是冯诺依曼熵。

值得注意的是文中讨论了多比特门和测量的作用方式的不同：
对于系统的一个bipartition（对应的冯诺依曼熵为），多比特门如果不同时作用在来自两个subsystem的比特上，则不会增加。
而subsystem内的测量则可能会改变。

基于coherent info的一个小计算

首先文中使用channel capacity计算了在一个bipartition中，对其中一个子系统进行随机测量的后果。
可以refer to之前读过的John Preskill 的讲义第十章。
这里采用的是一个简单的两部分模型：

和都包含个比特。和之间的纠缠可以用个比特描述。

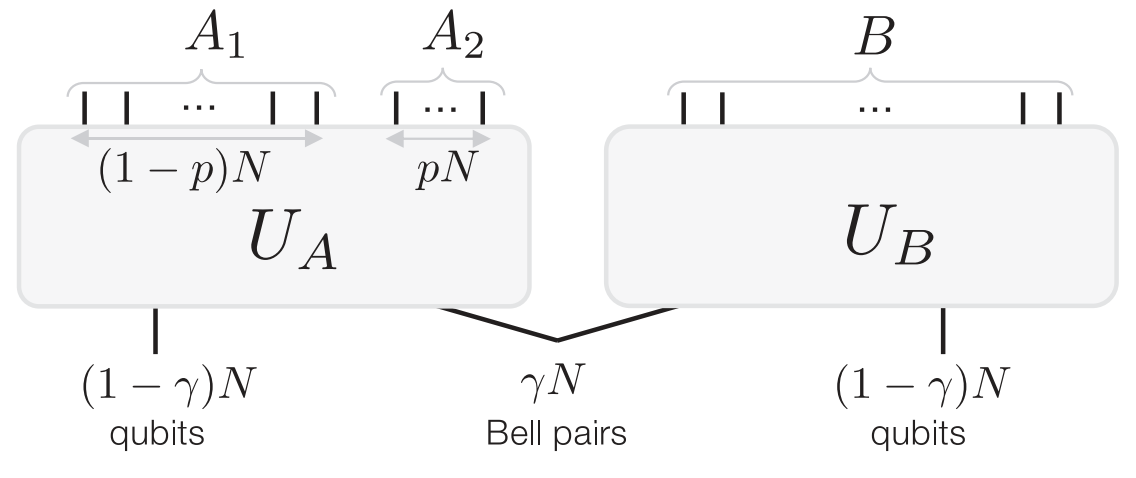
这里根据John Preskill的讲义中的decoupling theorem，得到一个bound：

$$\mathbb{E}_{U_{A}}\left[\left\|\rho_{A_{2} \tilde{B}}\left(U_{A}\right)-\rho_{A_{2}}^{\max } \otimes \rho_{\tilde{B}}\right\|_{1}\right] \leq 2^{-(1-2 p-\gamma) N / 2}$$

不等式左边是实际的态和完全decouple的态之间的距离。
右边的项意味着，只要被测量的比特（）不超过总比特数（）的一半，decouple就可以被bound住。这个bound也可以写成：

$$\gamma < 1-2p$$

而这篇文章做了一个简单的modified bound：通过考虑测量的过程，引入代表测量设备的额外个比特（系统），计算总的coherent information。
此时中包含的测量得到的经典信息也被包含进去了。
因此修改之后更强的bound：

$$\gamma <1-p$$

Model and Results

与QEC的联系

Page State

Page state是一类随机的纯态：

$$|\Psi \rangle = \sum_i^{L_A} \sum_j^{L_B} X_{ij} |\Psi_i^{(A)}\rangle |\Psi_j^{(B)}\rangle$$

系数是满足高斯分布的复数。
通过对Page state取partial trace，得到的混合态就是random induced mixed state.

Entanglement Features

描述一个写成tensor形式的unitary gate的entanglement性质，可以食用entanglement feature。