John Preskill 讲义Chap 10 Quantum Shannon Theory

关于量子信息的经典讲义。

1. From Classical Shannon Entropy to Von Neumann Entropy

Classical Shannon Entropy: , is an ensemble.

Quantum Von Neumann Entropy: , is a mixed state.

• Relation: if are orthogonal to each other, then the entropy equals to the corresponding classical entropy. .

---

• : majorizes . is at least as random as . That means for a doubly stochastic matrix .
• Doubly stochastic matrix: A square matrix of nonnegative real numbers, with each rows and columns sums to 1.

• Schur concavity: and , if , then .

• For that realizes , we have , then . Quantum entropy is less than or equal to the corresponding classical entropy. The equality holds when all the are orthogonal.

---

Project onto an orthogonal basis:

$$q(y) = \langle y|\rho |y \rangle = \sum_a |\langle y|a \rangle|^2\lambda_a, \quad \text{where} \quad \rho = \sum_a \lambda_a |a \rangle \langle a |$$

Here is the basis where is diagonal. Since is a doubly stochastic matrix, and therefore , where equality holds only if the measurement is in the basis .

• Mathematically: for a nondiagonal and nonnegative Hermitian matrix, the diagonal elements are more random than the eigenvalues.

From Pure States to Mixed States

Entanglement Concentration and Dilution

Concentration: From prepare maximally entangled states (e.g. two bits Bell pairs).

Dilution: From maximally entangled states prepare .

Asymptotically,

• Entanglement cost : create many copies of by consuming pairs of Bell states. “Entanglement dilution”
• Distillable entanglement : convert many copies of to Bell pairs. “Entanglement concentration”
• $E{D}(|\psi\rangle) \leq E{C}(|\psi\rangle)$, for bipartite pure states the equality holds.
• For pure states, $EC(|\psi\rangle{AB}) = ED(|\psi\rangle{AB}) = H(\rho_A) = H(\rho_B)$.

Quantify Mixed-state Entanglement

and are natrual and operationally meaningful ways to quantify entanglement. For pure states, entanglement dilution and concentration are asymtotically reversible, and equal to the Von Neumann entropy. Then this becomes a good measure for pure-state entanglement. However for mixed states, these two are asymptotically irreversible.

With only LOCC the dilution of mixed states is irreversible. However, if all bipartite operations that are incapable of creating entanglement (these operations include LOCC as well as some other operations) are included, the dilution and concentration of mixed states become asymptotically reversible again. (Related to quantum source theory.)

Accessible Information

Alice sends the information with a quantum ensemble . Bob perform a POVM on the state from Alice. Conditional possibility of Alice sent and Bob measured is , and the joint possibility is .

The information gain of Bob is represented by the change of Von Neumann entropy before and after the measurement. That is the mutual information:

$$I(X:Y) = H(X) -H(X|Y) = H(X) +H(Y) -H(XY)$$

Bob’s optimal choice of maximizes the information gain, and is defined as accessible information:

$$\operatorname{Acc}(\mathcal{E})=\max _{\boldsymbol{E}} I(X ; Y)$$

If the states in the ensemble are orthogonal and Bob has chosen the projectors to the basis, then . Otherwise, .

• Holevo bound: .
• Monotonity of Holevo bound: If is a quantum channel, then and therfore .

Classical capacity of a channel: can be expressed in terms of the optimal correlation between input and output for a single use of the channel,
.

Quantum channel capacity and Decoupling

The quantum capacity of a quantum channel is still a work in progress. Supose Alice prepare the state times in a code space , and use the quantum channel n times to send them to Bob. With decoding Bob attempt to get . The rate of the code is the number of encoded qubits sent per channel use:

$$R = \log_2 \text{dim}(\mathcal{H}^{(n)})$$

We say that is achievable if there is a sequence of codes such that with increasing , for any the rate is at least and Bob’s recovered state has fidelity .

The quantum channel capacity is the supremum of all achievable rates, i.e. the largest achievable rate over all possible codes.

Coherent information

There is a regularized formula of .

For any channel , it has an isometric Stinespring dilation with as the channel’s enviornment. And for any $\rhoA\psi{RA}\rhoA = \text{tr}_R(|\psi\rangle \langle \psi|)\psi{RA}\phi_{RBE}$. This could be represented as this graph:

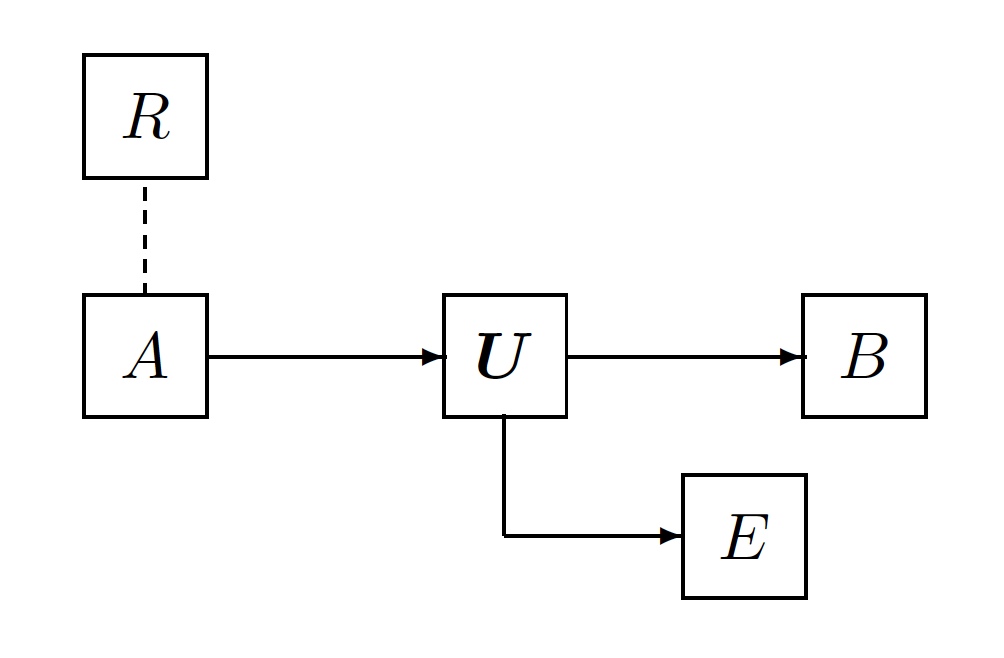
Stinespring dilation: Any channel has an isometric extension, the Stinespring dilation . We can obtain by tracing out the enviornment from . Since the unitary does not change the eigenvalues of the density matrix, the entropy of is preserved: . However the channel may not preserves the entropy. This dilation could be considered as the purification of a quantum channel.

We then define the one-shot quantum capacity of the channel:

$$Q_{1}(\mathcal{N}):=\max _{A}\left(-H(R | B)_{\phi_{R B E}}\right)$$

The max is taken over all possible $\rhoAH(R|B) = H(RB) - H(B) = H(E)-H(B)H(RB)=H(E)\phi{RBE}$ is a pure state.)

is an important quantity in quantum information, and it is called coherent information, denoted by $Ic(R\rangle B){\phi}$. This quantity is independent of the purification and the dilation. An alternative way of definition using mutual information:

$$I_c(R\rangle B)_{\phi} = \frac{1}{2} (I(R;B)-I(R;E)) = H(B)-H(E)$$

where:

$$\begin{aligned} &I(R ; B)=H(R)+H(B)-H(R B)=H(R)+H(B)-H(E) \\ &I(R ; E)=H(R)+H(E)-H(R E)=H(R)+H(E)-H(B) . \end{aligned}$$

So asymptotically the quantum channel capacity is:

$$\mathcal{Q}(\mathcal{N}^{A\to B}) = \lim_{n\to \infty} \max_{A^n} \frac{1}{n} I_c(R^n \rangle B^n)_{\phi_{R^n B^n E^n}}$$

where the input state is allowed to be entangled between times of channel uses.

If the coherent information is subadditive, then . However sometimes the coherence information is superadditive.

The decoupling principle

Quantum data-processing inequality: A quantum channel cannot increase the coherent information:

Suppose is followed by , since the mutual information is monotonic:

$$I(R;A) \geq I(R;B)\geq I(R;C)$$

then we can derive:

$$I_{c}(R\rangle A) \geq I_{c}(R\rangle B) \geq I_{c}(R\rangle C)$$

Now consider the situation of error correction codes. Two channels acting in succession on the code state $\rhoA\mathcal{N}^{A\to B}\mathcal{D}^{B\to \hat{B}}U^{A\to BE}V^{B\to \hat{B}B’}\psi{R\hat B}\chi_{B’E}$.

$$\psi_{R A} \stackrel{\boldsymbol{U}}{\longrightarrow} \phi_{R B E} \stackrel{\boldsymbol{V}}{\longrightarrow} \tilde{\psi}_{R \hat{B} B^{\prime} E}=\psi_{R \hat{B}} \otimes \chi_{B^{\prime} E}$$

The process is depicted in the graph:

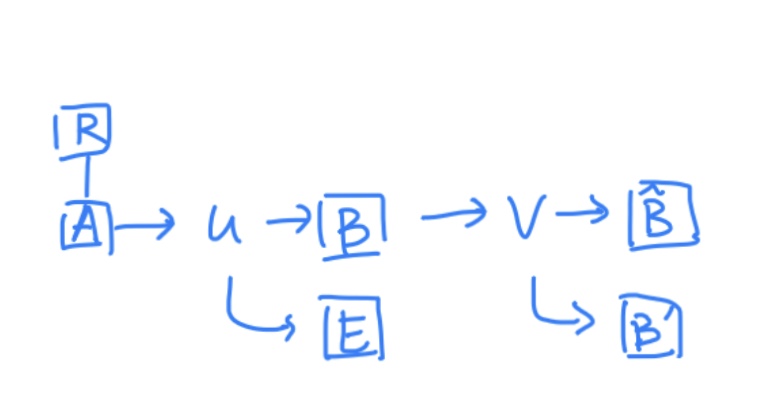
With perfect decoding Bob gets the state in as the purification of , and the coherence information is unchanged:

$$H(R) = I_c(R\rangle A) = I_c(R\rangle \hat B)$$

According to the quantum data-processing inequality, for the intermediate state in $RBE,

$$I_c(R\rangle B)= I_c(R\rangle A) = I_c(R\rangle \hat B)=H(R)=H(B)-H(E)$$ $$H(B) = H(RE) = H(R) + H(E)$$

This means the state is separable between and . Then in $\phi{RBE}\rho{RE}\rho_R \otimes \rho_E$.

This implies that purified quantum information transmitted through the noisy channel is exactly correctable if and only if the reference system is completely uncorrelated with the channel’s environment, or decoupled from the environment. This is the decoupling principle.

Now we have: exact correctability corresponds to exact decoupling. Further we can likewise see that approximate correctability corresponds to approximate decoupling.

For example is close to productstate in the norm:

$$\left\|\boldsymbol{\rho}_{R E}-\boldsymbol{\rho}_{R} \otimes \boldsymbol{\rho}_{E}\right\|_{1} \leq \varepsilon$$

norm: .
Fidelity written in norm: .

Next we provr that if these two density operators are close in norm ,then they also have fidelity close to 1.

Any purification of can be the product state with an isometry:

$$\tilde{\phi}_{R B E}=\boldsymbol{W}_{B}\left(\tilde{\psi}_{R B_{1}} \otimes \chi_{B_{2} E}\right)$$

So the fidelity of them:

$$\begin{aligned} F\left(\boldsymbol{\rho}_{R E}, \boldsymbol{\rho}_{R} \otimes \boldsymbol{\rho}_{E}\right)&=\left\|\left\langle\phi_{R B E} \mid \tilde{\phi}_{R B E}\right\rangle\right\|^{2} \\&\geq 1-\left\|\boldsymbol{\rho}_{R E}-\boldsymbol{\rho}_{R} \otimes \boldsymbol{\rho}_{E}\right\|_{1} \\ &\geq 1-\varepsilon \end{aligned}$$

And with the following conditions:

• Fidelity is monotonic, both under tracing out and under decoding map.
• could be decoded perfectly.

We can conclude that:

$$F\left(\mathcal{D}^{B \rightarrow \hat{B}}\left(\boldsymbol{\rho}_{R B}\right), \psi_{R \hat{B}}\right) \geq 1-\varepsilon$$

Thus approximate decoupling in the L1 norm implies high-fidelity correctability.