论文：VQE的经典复杂度分析

是关于一篇以前读过的2020年的Nature Physics论文的复习。作者是Sergey Bravyi等人。

1. Intro和结论

求量子算符的平均值的问题大概可以写成如下形式：n比特量子线路中测量厄米算符的平均值为:

$$\mu \equiv \langle 0^n|U^\dagger \hat O U|0^n\rangle \tag{1}$$

计算算符的平均值在量子计算中应用很广。比如VQE(variational
quantum eigensolver)、量子模拟和量子机器学习。

为了了解在计算量子算符平均值问题上，量子计算机是否优于经典计算机，这篇论文探讨了不同的经典算法下平均值问题关于线路深度、量子比特关联度以及的结构的计算复杂度。

这篇论文得到的结果是，至少浅层量子计算系统也许没有人们之前所考虑得那么powerful。对于2D和3D量子比特系统中constant-depth线路用特定经典算法模拟平均值计算的复杂度仅为和。为了在平均值问题上超越经典模拟，需要super-constant depth的量子线路（比如），或者不能被2D网格局域描述的量子比特关联，或者是求不能被poly(n)的算符张量积线性组合所描述的算符的平均值。

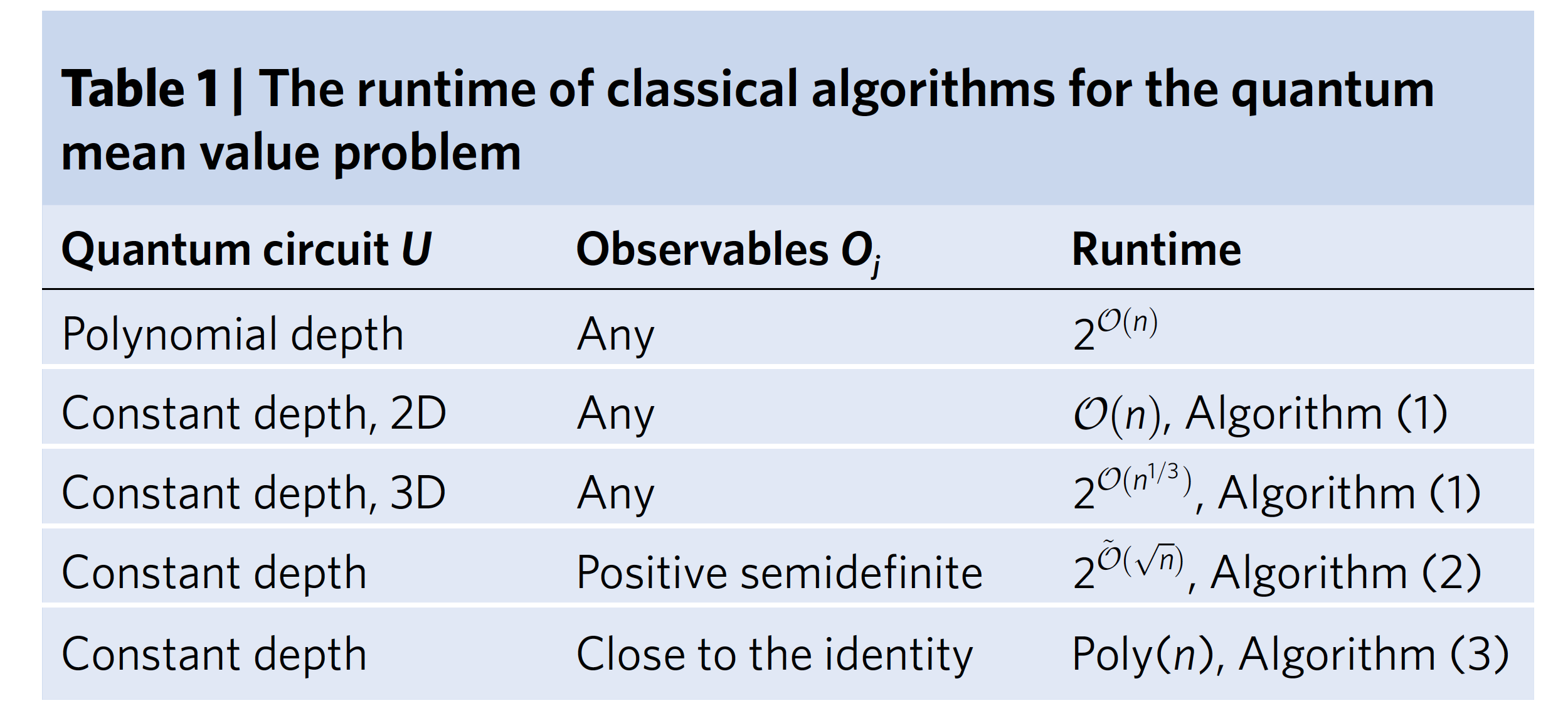
论文的主要结论如下表：

2. 因果律与光锥

有限深的量子线路中，假设信息的传播速度是一定的（即每一层线路的关联长度是一定的），那么信息就仅仅在光锥中传递。光锥的大小取决于线路的深度。

具体地来说，设是层的单比特和双比特门构成的线路，每一层内的门都作用在互不重叠的比特上。设$\mathcal Aj$是关于仅仅非平凡地作用在第个比特上的所有比特算符的一个代数。比特的一个子集就被称为是比特的一个光锥。需要满足以下条件：定义局域化的线路$U{loc}U\mathcal L(j)$以外的比特的门的线路。那么就有：

$$U^{\dagger} O U=U_{\mathrm{loc}}(j)^{\dagger} O U_{\mathrm{loc}}(j) \text { for all } O \in \mathcal{A}_{j}\tag{2}$$

也就是说对于中单比特算符的平均值的计算可以在更有限的光锥中计算，而光锥外的门对均值没有影响。或者说，仅仅非平凡地作用在光锥中的这些比特上。如果只有单、双比特门，那光锥的尺度由线路深度限制.后文中考虑的系统可以定义在图上，每一个顶点上放置比特且比特间的门仅仅作用在图上相邻的顶点间。定义范围来描述的的局域性：的范围定义为满足的邻域能够包括比特所有的光锥的最小整数。或者说，在图上和中任意比特最大距离为。

3. 算法1

根据因果律定理，可以将$\mu=\left\langle 0^{n}\left|U^{\dagger} O{1} \otimes \cdots \otimes O{n} U\right| 0^{n}\right\rangle$的平均值简化为：

$$\mu=\left\langle 0^{n}\left|U_{A}^{\dagger} U_{B}\right| 0^{n}\right\rangle \tag{3}$$

（如何简化，在后文讨论）
这样，就可以将其写成概率分布和一个复数函数的形式，然后应用蒙特卡洛方法去估计了：

$$\mu=\sum_{x \in\{0,1\}^{n}}\left\langle 0^{n}\left|U_{A}^{\dagger}\right| x\right\rangle\left\langle x\left|U_{B}\right| 0^{n}\right\rangle=\sum_{x \in\{0,1\}^{n}} \pi(x) F(x) \tag{4}$$

其中$\pi(x) = \gammaA^{-1}|\langle x|U_A|0^n \rangle|^2F(x)=\gamma{A}\left\langle x\left|U{B}\right| 0^{n}\right\rangle\left\langle x\left|U{A}\right| 0^{n}\right\rangle^{-1}|Oj|\leq 1\gamma{A} \equiv | U{A}|0^{n} \rangle |^{2} \leq 1\gamma{B} \equiv | U_{B}|0^{n}\rangle |^{2} \leq 1\mu\pi(x)F(x)$的期望了。

根据切比雪夫不等式，多次独立重复试验估计的值为：

$$\tilde{\mu}=S^{-1} \sum_{i=1}^{S} F\left(x^{i}\right) \tag{5}$$

其中为独立重复的次数，.对进行抽样以及计算需要经典算法能够模拟投影到的测量和计算振幅和。由于和的结构，这些计算可以在时间内完成。（在文后附的Methods一节有简单文字介绍，在后面讲。）

3.1 和的构造

首先，将2D的量子比特阵列分割成竖条${Ai}{B_i}$，效果如下图：

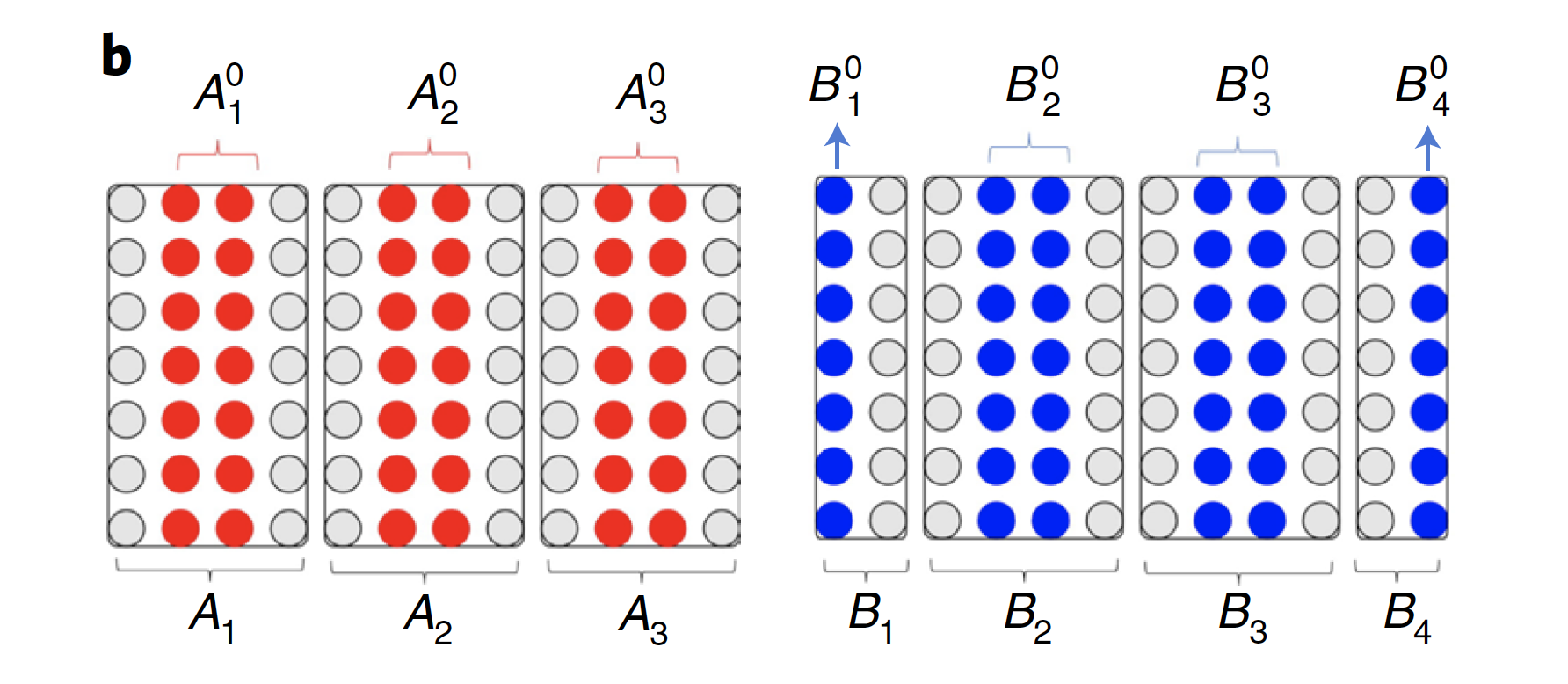
其中每一个和的宽度都为，而和都位于对应的竖条中央，宽度都为。这样就可以确保，和中的每一个比特的光锥，都位于对应的和内部。因此对仅仅非平凡地作用于第个比特的算符$O(j)=O{j} \otimes I_{\text {else}}$来说，有：

$$U_{A, i} =\prod_{j \in A_{i}^{0}} U_{\operatorname{loc}}(j)^{\dagger} O(j)^{\dagger} U_{\operatorname{loc}}(j) \text { and }\tag{6}$$ $$U_{B, i} =\prod_{j \in B_{i}^{0}} U_{\operatorname{loc}}(j)^{\dagger} O(j) U_{\mathrm{loc}}(j)\tag{7}$$

那么中的和就是：

$$U_{A}=\bigotimes_{i} U_{A, i} \text { and } U_{B}=\bigotimes_{i} U_{B, i}\tag{8}$$

可以通过因果律定理证明，$U{A}^{\dagger} U{B}=\prod{j=1}^{n} U^{\dagger} O(j) U=U^{\dagger}\left(O{1} \otimes \cdots \otimes O_{n}\right) U$。

3.2 关于计算复杂度的比较

与最好的张量网络算法相比，论文中的算法1在2D和3D情况下的复杂度：

	算法1	张量网络
2D
3D

其中，是算法1需要模拟的比特数。

3.3 计算：准一维线路的态矢模拟

这里是一种计算准一维线路的一种经典算法。前面出现的$UA, U_BU{A,i}mU_{A,i}(6)m$层。模拟是按照比特编号逐个进行模拟。每一个比特的模拟步骤如下：

• 将比特加载到模拟器，立刻初始化成；
• 把对其有非平凡作用的算符一层一层作用上去；
• 立刻对其进行测量，测量结束就立刻将其移出模拟器。

设为每一步加载到模拟器中的最大量子比特数目，。态矢模拟器的每一次门操作/测量操作都需要的时间。这样，整个的模拟复杂度就是.外推到3D的情况就是（使用了一个的register）。

根据下图所示简单的几何，可以得到。（严重怀疑这里给错了，因为根据他的“简单的几何”，我得到.）

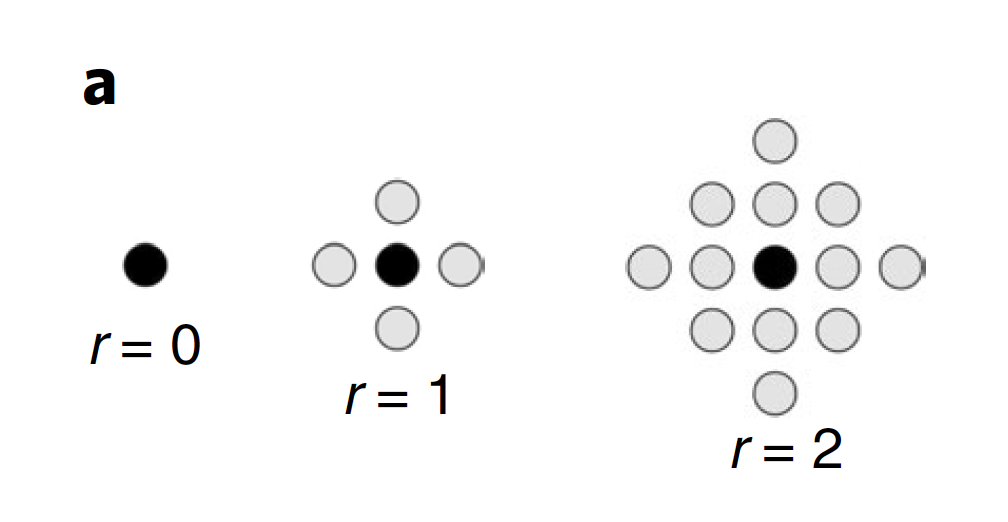
4. 关于估计误差

本文中讨论的估计误差，都是指的可加误差，即。但是还存在另一种误差的定义：相对误差，即。根据在0附近，显然相同数值的相对误差和可加误差至少需要同样的计算量。实际上这个问题是#P Hard的，因此对于constant-depth线路和是困难的。